В декартовых координатах проекции частного двух векторов вычисляются следующим образом.
Имеем
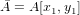
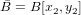
Частное этих векторов выражается формулой
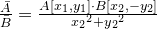
Иными словами, результате преобразований, в числителе мы получим произведение двух векторов, подчиняющееся уже известным правилом, а в знаменателе – число.
Обратите внимание на знак при y2. При вычислении частного двух векторов, представленных в виде проекций, этот знак всегда следует изменить на противоположный.
 Почему получается именно так? Дело в том что, прежде всего, следует избавиться от мнимых значений в знаменателе и получить деление вектора на действительное число.
Для применяют искусственный приём, умножая и числитель дроби на сопряжённое знаменателя. Сопряжённое комплексного числа – это комплексное число (вектор),
точки которого симметричны точкам исходного вектора относительно оси ОХ (рис. 10). Сопряжённое обозначается значком " ~ " (тильда) сверху.
Почему получается именно так? Дело в том что, прежде всего, следует избавиться от мнимых значений в знаменателе и получить деление вектора на действительное число.
Для применяют искусственный приём, умножая и числитель дроби на сопряжённое знаменателя. Сопряжённое комплексного числа – это комплексное число (вектор),
точки которого симметричны точкам исходного вектора относительно оси ОХ (рис. 10). Сопряжённое обозначается значком " ~ " (тильда) сверху.
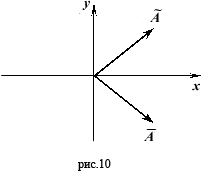 Таким образом, если имеется вектор
Таким образом, если имеется вектор 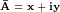 , то его сопряжённым будет , то его сопряжённым будет
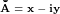 . Умножая числитель и знаменатель дроби на сопряжённое знаменателя, получаем . Умножая числитель и знаменатель дроби на сопряжённое знаменателя, получаем
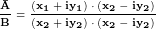
Раскрывая скобки (обратите внимание на формулу разности квадратов в знаменателе) и проведя элементарные преобразования, получаем приведённое выше
выражение для частного двух векторов в декартовой системе координат.
5. Круг балансировщика
5.1. Что такое круг балансировщика
Прибегать к графическим построениям и действиям над векторами в полярной системе координат специалисту-балансировщику приходится постоянно.
Чтобы не откладывать на листе бумаги векторы при помощи линейки и транспортира, что неудобно, применяют так называемые круги балансировщика.
Это специальные заготовки на листах формата А4, представляющие собой сетку из концентрических окружностей, по которым отсчитывают длину отрезка в выбранном масштабе, и
радиальных отрезков, соответствующих углам от 0° до 360°. Постепенно оттачиваясь с годами, круг балансировщика постепенно принял тот удобный и компактный вид, в котором он
изображён на рис. 11. Это простейшее приспособление является комфортной средой для построения любых векторов и проведения с ними арифметических действий.
Опытный балансировщик всегда имеет при себе с десяток таких кругов, независимо от наличия у него программного обеспечения для балансировки.
Положив перед собой два или несколько кругов балансировщика, хороший специалист способен графически решить практически любую задачу, встречающуюся в его деятельности.
При желании можно научиться работать с кругами и в электронном виде, строя векторы, например, в среде Microsoft Office Word. Где взять заготовки кругов балансировщика?
Конечно, можно самому создать их на компьютере при помощи одного из графических редакторов, но для этого потребуется недюжинная усидчивость и хорошая компьютерная подготовка.
Гораздо проще бесплатно скачать круги на сайте http://www.vibrorotor.ru в разделе поддержки и распечатать их в любом количестве.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|

 Таким образом, если имеется вектор
Таким образом, если имеется вектор 