3. Декартова и полярная системы координат
В науке о балансировке деталей и узлов, получившей название балансировочной техники, векторы изображаются в полярной или в декартовой системе координат, хотя существует множество других координатных систем.
В полярной системе координат вектор характеризуется длиной радиус-вектора и углом, который он образует с осью OX.
Направление отсчёта угла принято против часовой стрелки. Единого стандарта записи векторов для полярной системы координат не существует.
Можно, например, встретить написание одного и того же вектора с модулем 20 и углом 30° в виде "20~30°", "20∠30°" и т.п. Принципиальной разницы здесь нет.
Мы будем записывать векторы в виде дроби: Ā = A / φ. Знак дроби здесь не имеет отношения к операции деления. Он лишь отделяет модуль вектора A от его угла φ.
Например, чтобы изобразить в полярных координатах вектор 30 / 45° (рис.2), следует при помощи транспортира отложить угол 45°, после чего провести отрезок соответствующей длины в
выбранном масштабе.
 В декартовых координатах вектор задаётся в виде пары чисел (x, y), которые являются проекциями вектора на оси координат x и y.
В математике принята так называемая алгебраическая форма записи вектора. Она выражается в виде комплексного числа:
В декартовых координатах вектор задаётся в виде пары чисел (x, y), которые являются проекциями вектора на оси координат x и y.
В математике принята так называемая алгебраическая форма записи вектора. Она выражается в виде комплексного числа:
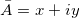
, где
x - проекция вектора на ось X;
y - проекция вектора на ось Y;
i - мнимая единица 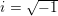
Читателю, который мало сталкивался с математикой, не следует опасаться непривычной формы записи и термина «мнимая единица». В данном случае i – это всего лишь отличительный признак
проекции на вертикальную координатную ось y. Например, для построения вектора Ā = (20 + 30i) следует отложить на соответствующих осях координат 20 и 30 единиц в
выбранном масштабе, затем провести линии, параллельные осям, после чего, соединяя центр системы координат с пересечением линии, построить вектор Ā (рис. 3).
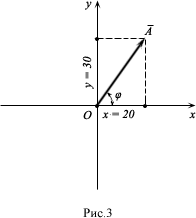 Модуль вектора находится по теореме Пифагора:
Модуль вектора находится по теореме Пифагора:
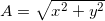
Угол между линией вектора и осью ОХ определяется из решения прямоугольного треугольника:
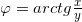
В технической литературе часто можно встретить форму записи комплексного числа без знака мнимой единицы. Координаты конца вектора задаются в квадратных скобках:
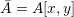 . .
Итак, полярная система координат удобна при решении задач графическим методом, а декартова система больше подходит для создания математических моделей
и написания компьютерных программ.
Постижение практических начал балансировки деталей и узлов зиждется на основах векторной алгебры. Запомните это.
 Здесь и далее мелким шрифтом мы будем выделять материал необязательный для всех читателей, но
необходимый при углублённом изучении предмета. Такой материал будет помечен значком профессорской шапочки. Здесь и далее мелким шрифтом мы будем выделять материал необязательный для всех читателей, но
необходимый при углублённом изучении предмета. Такой материал будет помечен значком профессорской шапочки.
В своей практической деятельности балансировщик имеет дело главным образом с полярной системой координат, где вектор представлен модулем и углом с осью ОХ. Но для более полного
понимания предмета ему необходимо иметь представление и о действиях с проекциями векторов на оси. Любой изучаемый предмет следует рассматривать в целом, а не кусками, вырезанными
из контекста.
Проекция на ось ОХ называется действительной частью комплексного числа и обозначается Re, а проекция на ось OY – мнимой частью комплексного числа и обозначается Im.
Сами же комплексные числа носят название мнимых чисел в отличие от действительных чисел – чисел, с которыми мы имеем дело в повседневной практике.
Это исторически сложившееся название. На самом деле мнимые числа ничуть не менее реальны, чем действительные. Действия над векторами аналогичны действиям над комплексными числами.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|

 В декартовых координатах вектор задаётся в виде пары чисел (x, y), которые являются проекциями вектора на оси координат x и y.
В математике принята так называемая алгебраическая форма записи вектора. Она выражается в виде комплексного числа:
В декартовых координатах вектор задаётся в виде пары чисел (x, y), которые являются проекциями вектора на оси координат x и y.
В математике принята так называемая алгебраическая форма записи вектора. Она выражается в виде комплексного числа: 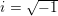
 Модуль вектора находится по теореме Пифагора:
Модуль вектора находится по теореме Пифагора: