
Рис.14
Выделяем окружность диаметром, соответствующем 30 г, в том же масштабе. Где-то на этой окружности будут находиться концы искомых вектор-масс.
При помощи циркуля чертим такую же окружность с центром в конце исходного вектора 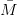 .
Точки пересечения двух окружностей будут соответствовать концам векторов .
Точки пересечения двух окружностей будут соответствовать концам векторов 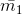 и
и 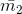 . .
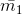 = 30 г / 22° = 30 г / 22°
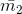 = 30 г / 118° = 30 г / 118°
Разумеется, эта задача имеет смысл только при соблюдении условия m1 + m2 ≥ M, ведь из двух грузов по 10 г никогда не удастся получить груз 30 г!
У читателя может возникнуть вопрос, как поступить, если в канавке имеются три груза, а не два (рис.13). В таких случаях обычно раскладывают исходную вектор-массу на два груза , а затем
один из этих грузов подвергают разложению ещё раз.
Пример 3.Для проведения балансировки, в плоскости коррекции ротора требуется установить груз массой 45 г на углу 335°. В распоряжении балансировщика имеются только
два груза: m1 = 55 г и m2 = 22 г. Найти такое взаимное положение имеющихся грузов на плоскости коррекции, чтобы обеспечить
соблюдение указанного выше требования.
Решение. Условием решения этой задачи будет равенство 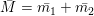 .
Решаем задачу графическим способом. Задавшись удобным масштабом, на круге балансировщика строим вектор .
Решаем задачу графическим способом. Задавшись удобным масштабом, на круге балансировщика строим вектор 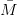 ,
соответствующий требуемому грузу (рис.15). Выделяем две окружности 1 и 2, на которых будут находиться концы искомых вектор-масс ,
соответствующий требуемому грузу (рис.15). Выделяем две окружности 1 и 2, на которых будут находиться концы искомых вектор-масс
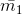 = 30 г / 22° = 30 г / 22°
и 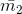 . .
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|


