
Рис.5
4.2. Вычитание векторов
Для графического вычисления разности векторов в полярной системе координат также применяется правило треугольника или правило параллелограмма. В первом случае конец
вычитаемого вектора следует соединить с концом вектора уменьшаемого. При необходимости можно осуществить параллельный перенос результирующего вектора в начало координат (рис. 6, а).

Рис.6
а - вычитание векторов по правилу треугольника
б - вычитание векторов по правилу параллелограмма
Вычитание по правилу параллелограмма более наглядно, хотя и чуть более громоздко1. Разность векторов представляется как
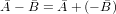 . Очевидно, что вектор с отрицательным знаком - это тот же вектор,
но развёрнутый на 180°.
После построения вектора . Очевидно, что вектор с отрицательным знаком - это тот же вектор,
но развёрнутый на 180°.
После построения вектора 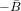 дальнейшие
действия полностью повторяют действия, описанные в правилах сложения векторов (рис 6, б). дальнейшие
действия полностью повторяют действия, описанные в правилах сложения векторов (рис 6, б).
В декартовой системе координат вычитание векторов полностью аналогично их сложению, только координаты проекций при этом не складываются, а вычитаются (рис. 7).
1 Практика показывает, что балансировщики, только начинающие осваивать вычитание векторов
графическим методом, часто путают направление результиующего вектора, если пользуются методом треугольника. Но для тех, кто уже имеет опыт работы с векторами, приприменение правила
параллелограмма в данном случае является только излишним усложнением построений.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|



