2. Понятие вектора в балансировке. Центробежная сила.
Почти все величины, с которыми мы будем сталкиваться в этой книге при изучении процесса балансировки – векторные. Вектор – это величина, которая характеризуется не только
своим численным значением, но и направлением, в отличие от скаляра, который характеризуется только значением. Векторные величины обозначаются стрелочкой или чёрточкой сверху. К примеру,
груз, установленный в любой плоскости вращающейся детали (ротора), имеет свою величину (массу) и угол, на котором он
установлен относительно нулевой метки, нанесённой на поверхность ротора и соответствующей 0° (рис. 1а). Сочетание массы груза и угла его установки образует вектор, в балансировочной технике
иногда называемый вектор-массой (рис. 1б).

Рис.1
а - груз массой М, установленный на углу φ относительно нулевой метки
б - груз М, представленный в виде вектор-массы
Этот вектор вращается вместе с ротором, поэтому для наблюдателя, находящегося вне ротора, он является вектором вращающимся, а для гипотетического наблюдателя, расположившегося внутри
ротора и совершающего вращение вместе с ним - вектором неподвижным 1.
Приведём ещё пример. Переменную нагрузку на неподвижные опоры балансировочного станка порождает центробежная сила, которая также является векторной
величиной. Она равна произведению модуля (значения) неуравновешенной массы на вектор центростремительного ускорения, взятое с обратным знаком.
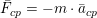
Центростремительное ускорение, если вспомнить школьный курс физики, представляется формулой
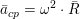
, где
ω - угловая скорость вращения ротора, с-1;
R - радиус, на котором находится неуравновешенная масса.
Отсюда
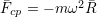
Таким образом центробежная сила будет являться вектором, направленным вдоль радиуса, а величина этой силы окажется пропорциональной квадрату угловой скорости вращения.
Векторами являются также дисбалансы, моменты сил, вибрации опор и другие величины, рассматриваемые при изучении процесса балансировки.
1 Это замечание связано с понятием об инерциальной и неинерциальной системах отсчёта. При рассмотрении процесса балансировки
удобнее пользоваться неинерциальной системой координат (наблюдатель находится внутри ротора и вращается вместе с ним). В этом случае мы можем рассматривать практически любой вектор
как постоянную величину при условии установившегося режима вращения привода станка и отсутствия внешних воздействий на ротор. Инерциальную систему координат (наблюдатель
глядит на вращающуюся систему извне) чаще используют при анализе колебаний, например, при вибродиагностике.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|


