
Рис.7
4.3. Умножение (деление) вектора на число
Здесь всё предельно просто. В полярной системе координат модуль умножается (делится) на число при сохранении угла, а в декартовой системе обе проекции умножаются (делятся) на это число.
4.4. Произведение двух векторов
Физический смысл операций сложения и вычитания векторов умозрительно понятен. Проиллюстрируем эти операции на примерах из практики балансировки.
Пусть в плоскости коррекции ротора была установлена масса M1 = 130 г / 60°.
Предположим, что впоследствии на ту же плоскость установили ещё одну массу M2 = 90 г / 120°. Требуется определить одиночную массу, эквивалентную
двум установленным. Очевидно, что искомый груз будет соответствовать векторной сумме M1 и M2:
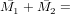 130 г / 60° + 90 г / 120°
= 191,6 г / 84°. Эта суммарная масса и должна быть установлена в плоскости коррекции ротора вместо двух исходных масс1. 130 г / 60° + 90 г / 120°
= 191,6 г / 84°. Эта суммарная масса и должна быть установлена в плоскости коррекции ротора вместо двух исходных масс1.
Другой пример. На опоре балансировочного станка была замерена вибрация
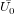 = 160 ед. / 45°.
После установки пробного груза, вновь зафиксированная вибрация составила = 160 ед. / 45°.
После установки пробного груза, вновь зафиксированная вибрация составила 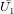 = 76 ед. / 90°.
Определить, какая дополнительная вибрация = 76 ед. / 90°.
Определить, какая дополнительная вибрация 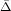 была вызвана установкой пробного груза.
После недолгих размышлений внимательный читатель ответит что была вызвана установкой пробного груза.
После недолгих размышлений внимательный читатель ответит что 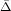 = =
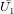 - - 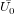 = 76 ед. / 90° - 160 ед. / 45° = 122,9 ед. / 195°, и будет совершенно прав2.
= 76 ед. / 90° - 160 ед. / 45° = 122,9 ед. / 195°, и будет совершенно прав2.
Перейдём к арифметическому произведению одного вектора на другой, которое также встречается в балансировочных расчётах, но физический смысл которого на первый взгляд неочевиден.
Определение произведения двух векторов звучит следующим образом.
Вектор A / α, умноженный на вектор B / β есть вектор C / γ, получаемый доворотом вектора A на угол β (соответственно γ = α + β)
и с модулем, равным A · B. Доворот производится в положительную сторону – в сторону увеличения угла.
Даже если логика этого определения пока покажется читателю несколько туманной, то в дальнейшем, например при изучении динамического коэффициента влияния – одной из основополагающих
величин в теории балансировочной техники, смысл векторного произведения станет совершенно понятным и не оставит никаких сомнений. Представление произведения векторов в
полярной системе координат выглядит очень просто (ещё раз напомним, что здесь косая черта является формой записи вектора и не имеет отношения к делению).
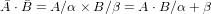
Модули перемножаются, а углы складываются (рис. 8). Вот и всё.
1В среде специалистов оставление на плоскости коррекции большого количества грузов
не принято. На профессиональном слэнге это называется "ёж" и свидетельствует о низком уровне подготовки или о неаккуратности балансировщика.
2Определение влияния пробного груза на вибрацию ротора лежит в основе всех балансировочных расчётов.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|


