4. Арифметические действия над векторами
С векторами, как и с обычными числами, можно производить все четыре арифметических действия. Действия эти настолько широко применяемы в практике балансировки,
что должны быть отработаны читателем буквально до автоматизма.
4.1. Сложение векторов
В полярной системе координат сложение векторов производится графически, по правилу параллелограмма или по правилу треугольника.
При применении первого способа, отложенные из одной точки О векторы нужно достроить до параллелограмма. Вектор суммы соединяет точку
начала координат О с противоположным углом полученного параллелограмма (рис. 4, а).
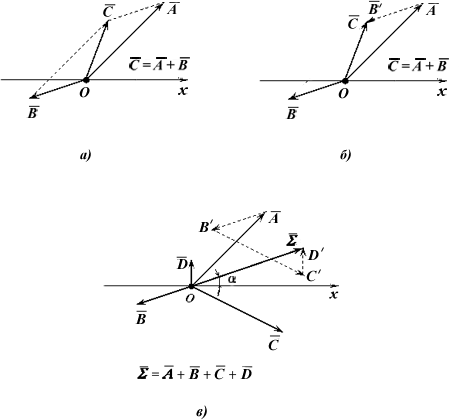
Рис.4
а - сложение двух векторов по правилу параллелограмма
б - сложение двух векторов по правилу треугольника
в - сложение нескольких векторов по правилу треугольника
Второй способ заключается в параллельном переносе одного из векторов, например вектора
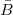 , в конец другого вектора (вектора , в конец другого вектора (вектора 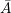 ).
Результирующий вектор суммы ).
Результирующий вектор суммы 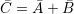 соединит начало координат О с
концом вектора соединит начало координат О с
концом вектора 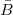 (рис.4, б).
Модуль результирующего вектора (рис.4, б).
Модуль результирующего вектора 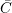 измеряется при помощи линейки, а угол α между вектором и осью OX - при
помощи транспортира. Таким образом, по правилу треугольника можно графически складывать любое количество векторов без промежуточных построений рис. 4, в).
Надо заметить, что если возникнет необходимость применения аналитического метода действий над векторами, то полярная система координат окажется неудобной.
Для этих целей, как уже было сказано, гораздо лучше подходит декартова система координат. измеряется при помощи линейки, а угол α между вектором и осью OX - при
помощи транспортира. Таким образом, по правилу треугольника можно графически складывать любое количество векторов без промежуточных построений рис. 4, в).
Надо заметить, что если возникнет необходимость применения аналитического метода действий над векторами, то полярная система координат окажется неудобной.
Для этих целей, как уже было сказано, гораздо лучше подходит декартова система координат.
В декартовой системе координаты суммарного вектора складываются из сумм проекций на оси векторов-слагаемых:
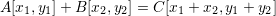 . .
Пример сложения двух векторов в декартовой стстеме приведён на рис. 5.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|


