
Рис.8
Остаётся лишь добавить, что в результате сложения углов векторов-сомножителей может получиться угол, больший 360°. Такими значениями углов в математике пользоваться не принято.
В таких случаях из полученного значения угла следует вычесть 360. Например,
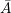 = 20 / 330°; = 20 / 330°;
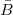 = 30 / 235°; = 30 / 235°;
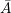 · ·
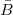 = 600 / 565° = 600 / (565 - 360)° = 600 / 205°. = 600 / 565° = 600 / (565 - 360)° = 600 / 205°.
В декартовой координатной системе перемножение векторов подчиняется зависимости
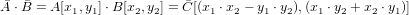 . .
 Поясним, как получается эта зависимость с точки зрения алгебры комплексных чисел.
Запишем перемножаемые векторы в комплексной форме.
Поясним, как получается эта зависимость с точки зрения алгебры комплексных чисел.
Запишем перемножаемые векторы в комплексной форме.
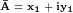
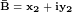 , где , где
i - мнимое число, 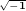 . .
Тогда
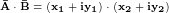
Раскрывая скобки, получаем
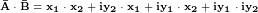 . .
Учитывая, что 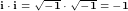 и, группируя действительные и мнимые части, имеем и, группируя действительные и мнимые части, имеем
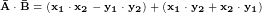 , что соответствует формуле умножения, приведённой выше. , что соответствует формуле умножения, приведённой выше.
4.5. Частное двух векторов
Рассматривая деление как действие, обратное умножению, для полярной системы координат запишем:
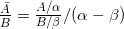
При вычитании углов в определённых случаях может получиться отрицательная величина, что выглядит некорректно. Тогда к полученному значению угла прибавляют 360°.
Таким образом, частным двух векторов А / α и В / β является вектор
С / γ, полученный поворотом вектора на угол β в сторону уменьшения угла (γ= α – β) и уменьшением его модуля в В раз (C = A / B).
Частное двух векторов в полярной системе координат показано на рис. 9.
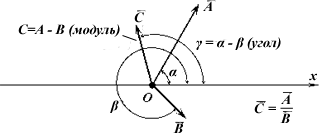
Рис.9
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|



