
Рис.14
Аналогично предыдущему примеру чертим вспомогательную окружность 2´ с центром в точке O´,
соответствующей концу вектора 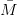 . Окружности 1 и 2´ пересекаются
в двух точках C и C´. Соединяем одну из точек пересечения двух окружностей, например, точку C
с концом вектора . Окружности 1 и 2´ пересекаются
в двух точках C и C´. Соединяем одну из точек пересечения двух окружностей, например, точку C
с концом вектора 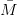 . Проводим отрезки O´D, параллельный OC, и
OD, достраивая параллелограмм OCO´D. Отрезок O´D будет соответствовать вектору . Проводим отрезки O´D, параллельный OC, и
OD, достраивая параллелограмм OCO´D. Отрезок O´D будет соответствовать вектору
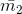 . Действительно, . Действительно, 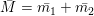 (сложение по правилу параллелограмма). Аналогичным образом, соединяя начало координат со второй точкой пересечения окружностей 1 и 1 (точка
C´) и достраивая параллелограмм ODO´C´, получаем ещё одно решение задачи - вектор
(сложение по правилу параллелограмма). Аналогичным образом, соединяя начало координат со второй точкой пересечения окружностей 1 и 1 (точка
C´) и достраивая параллелограмм ODO´C´, получаем ещё одно решение задачи - вектор
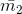 ´. ´.
Определив по сетке круга балансировщика соответствующие углы, получаем ответы:
- m1 = 55 г / 358°; m1 = 22 г / 230°
- m2 = 55 г /312°; m2 = 22 г / 80°.
Из приведённого решения вытекает ряд выводов:
- В данной постановке задача имеет два равноправных решения: пара вектор-масс (
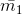 , ,
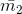 ) и пара вектор-масс ( ) и пара вектор-масс (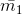 ´, ´,
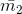 ´), симметричных относительно вектора ´), симметричных относительно вектора 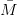 . .
- Для решения примера можно использовать в качестве вспомогательной как окружность 2´, так и 1´.
Ответы получились бы одинаковыми.
- Если основная и вспомогательная окружности не пересекаются, но соприкасаются, задача имеет единственное решение. Это произойдёт в случае, если
m1 + m2 = M
- Если построенные окружности не пересекаются и не соприкасаются между собой, то задача не имеет решений.
Мы привели пока лишь три примера графического решения задач из практики балансировки. Таких примеров может быть множество. Безусловно, многие программные пакеты включают в
себя утилиты, позволяющие избежать ручных вычислений в большинстве ситуаций. Но при том многообразии задач, с которым сталкивается балансировщик в своей работе,
предусмотреть соответствующую утилиту для каждого частного случая практически невозможно. Несмотря на это, специалист, свободно владеющий векторной алгеброй
и знакомый с основами геометрии, никогда не окажется бессильным даже в случае отсутствия в его распоряжении соответствующего программного обеспечения.
© Рубин Алексей Анатольевич 2013 г
Использование материала на своих ресурсах без разрешения автора запрещено!

|


